二、十、八、十六进制之间的转换
以下简称:
- 二进制:简称为 B,来自英文 "Binary"。
- 十进制:简称为 D,来自英文 "Decimal"。
- 八进制:简称为 O 或 Oct,来自英文 "Octal"。
- 十六进制:简称为 H,来自英文 "Hexadecimal"。
例如:
- (1010)B 表示一个二进制数。
- (1234)D 表示一个十进制数。
- (7643)O 或 (7643)Oct 表示一个八进制数。
- (A2F)H 表示一个十六进制数。
这些简称有助于在技术文档、编程语言以及讨论中快速指明数值所采用的进制系统。
在线进制转换工具:https://tool.lu/hexconvert/
二进制 ➔ 十进制
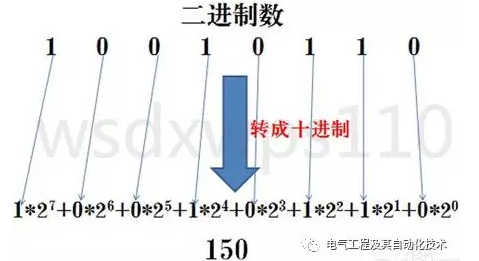
方法:按权展开相加。每个二进制位乘以其对应的权重(2的幂次方),然后将结果相加。
示例:将二进制数1101转换为十进制。
- 12^3 + 12^2 + 02^1 + 12^0 = 8 + 4 + 0 + 1 = 13
- 所以,(1101)B = (13)D
二进制 ➔ 八进制
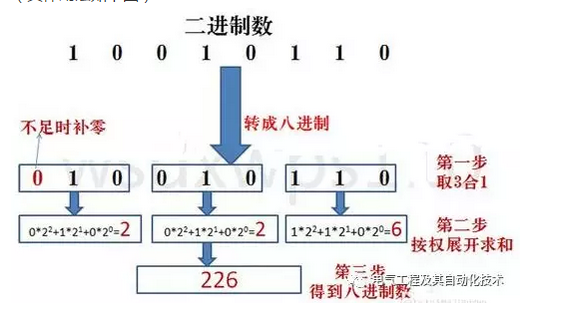
方法:每三位二进制数转换成一位八进制数,从右向左开始分组,不足补0。
示例:将二进制数101101转换为八进制。
- 分组:010 110 1 -> 补0后变为010 110 001
- 转换:2 6 1
- 所以,(101101)B = (261)O
二进制 ➔ 十六进制
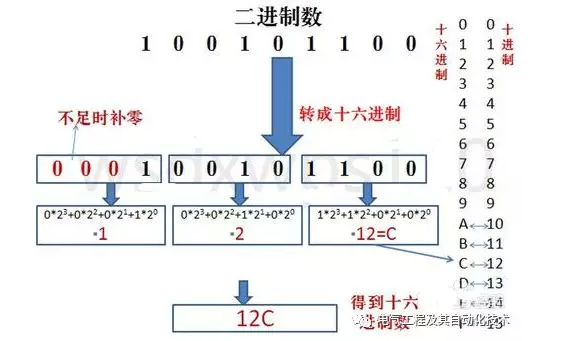
方法:每四位二进制数转换成一位十六进制数,从右向左开始分组,不足补0。
示例:将二进制数11010110转换为十六进制。
- 分组:1101 0110
- 转换:D 6
- 所以,(11010110)B = (D6)H
十进制 ➔ 二进制
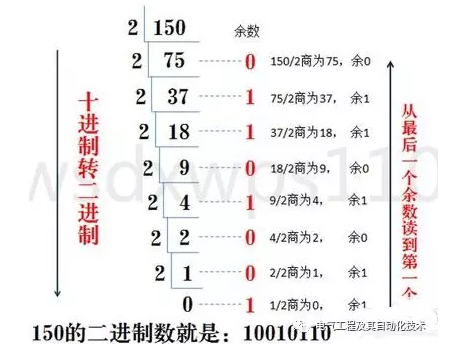
方法:采用“除2取余法”,即用十进制数不断除以2,记录每次的余数(从下往上读),直到商为0为止。
示例:将十进制数13转换为二进制。
- 13 ÷ 2 = 6 余 1
- 6 ÷ 2 = 3 余 0
- 3 ÷ 2 = 1 余 1
- 1 ÷ 2 = 0 余 1
- 所以,(13)D = (1101)B
八进制 ➔ 二进制
方法:每一位八进制数转换成三位二进制数,不足在最左边补零。
示例:将八进制数261转换为二进制。
- 转换:2 -> 010, 6 -> 110, 1 -> 001
- 结果:010 110 001
- 所以,(261)O = (101101)B
十六进制 ➔ 二进制
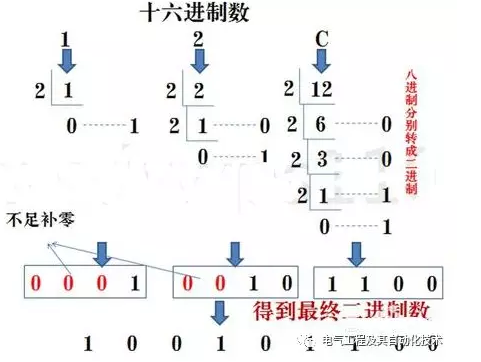
方法:每一位十六进制数转换成四位二进制数,不足在最左边补零。
示例:将十六进制数D6转换为二进制。
- 转换:D -> 1101, 6 -> 0110
- 结果:1101 0110
- 所以,(D6)H = (11010110)B
十进制 ➔ 八、十六进制
有两种主要方法进行转换:间接法和直接法。
间接法
- 将十进制数转换为二进制。
- 再将二进制数转换为八进制或十六进制。
直接法
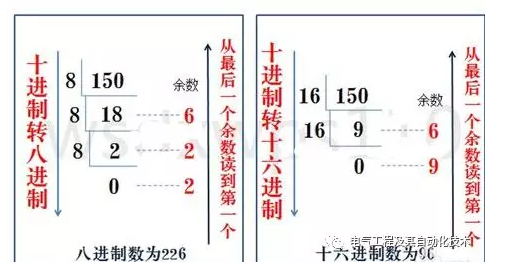
步骤:
- 对于转换为八进制,使用除8取余法;对于转换为十六进制,使用除16取余法,直到商为0为止。
示例(十进制到八进制):
- 将十进制数26转换为八进制。
- 26 ÷ 8 = 3 余 2
- 3 ÷ 8 = 0 余 3
- 结果:(26)D = (32)O(从下往上读取余数)。
示例(十进制到十六进制):
- 将十进制数26转换为十六进制。
- 26 ÷ 16 = 1 余 10(在十六进制中表示为A)
- 1 ÷ 16 = 0 余 1
- 结果:(26)D = (1A)H(从下往上读取余数)。
八、十六进制 ➔ 十进制

方法:将八进制或十六进制数按权展开相加得到十进制数。
示例(八进制到十进制):
- 将八进制数32转换为十进制。
- 38^1 + 28^0 = 24 + 2 = 26
- 结果:(32)O = (26)D。
示例(十六进制到十进制):
- 将十六进制数1A转换为十进制。
- 116^1 + 1016^0 = 16 + 10 = 26
- 结果:(1A)H = (26)D。
- 将八进制数32转换为十进制。
